Neural Network From Scratch With Python

Имплементация компьютерной нейронной сети с помощью Python

Всем привет. В предыдущей статье уже было упомянуто о том, что функция сигмоиды может использоваться как фукция активации компьютерной “нейронной сети”, сегодня рассмотрим алгоритм “нейронки” более подробно. Компьютерная “нейронная сеть” (Computer Neural Network) является алгоритмом машинного обучения, который за своим принципом напоминает работу нейронной сети человека. В двух словах условный “нейрон” - это функция (активации), которая принимает и отдает сигналы.

Изображение “нейрона” (математическая модель парсептрона)

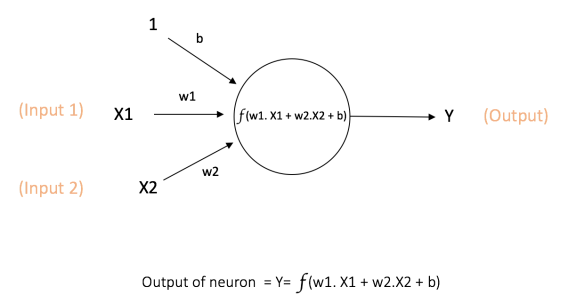
Нейроны-функции обьеденяются в слои, слоев может быть много и не очень, их расделяют на входной, скрытый(скрытые) и выходной, при этом нейронная сеть с одним скрытым (внутренним) слоем будет називатся однослойной.
Виглядит это примерно так:

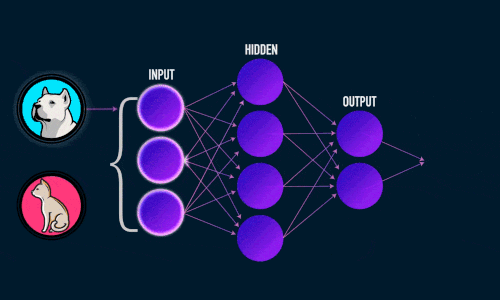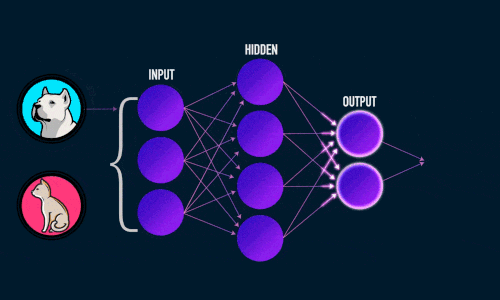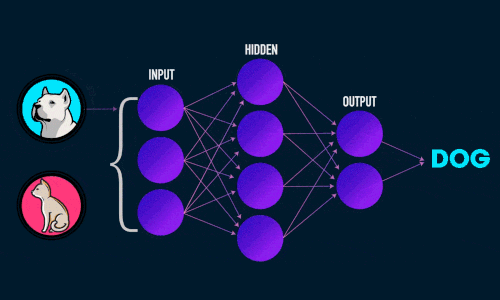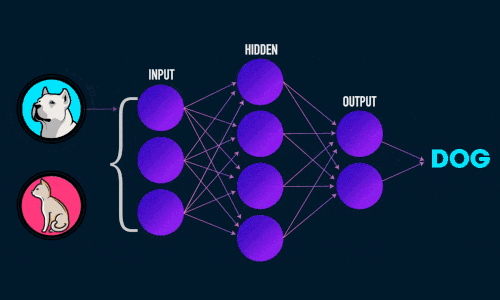
Нужно добавить, что рассматриваемая нейронная сеть относится к типу “обучение с учителем” (supervised learning) и решает задачу классификации.

Функция активации

Рассмотрим некоторые популярные функции активации.

Сигмоида

Как было сказано выше, функция сигмоиды часто используется как функция активации в нейронных сетях, наряду с гиперболическим тангенсои и ReLU(о которых поговорим ниже).

Ниже дана формула сигмоиды (в качестве примера степенной функции взята линейная регрессия):

$$z^{(i)} = w^T x^{(i)} + b$$ $$\hat{y}^{(i)} = a^{(i)} = sigmoid(z^{(i)})$$ $$sigmoid(z^{(i)}) = \frac{1}{1-e^{-z^{(i)}}}$$

Где
$z^{(i)}$ - степенная функция (линейная регрессия)
$\hat{y}^{(i)}$ - гипотеза
$sigmoid(z^{(i)})$ - сигмоида

Графичек:

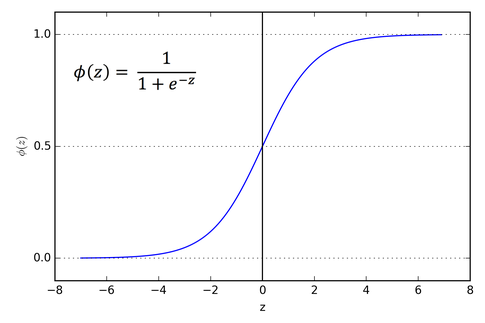
Преимущества сигмоиды:

• Гладкость: Имеет производную в любой точке, что является важным фактором при использовании метода градиетного спуска.

• Чуствительна к малейшим изменениям $x$ на участке от [-2;2], что позволяет четко провести границу между классами.

• Значения $y$ всегда находятся в диапазоне [0,1]

Недостатки:

• Стоимость вычислений, критично на устроиствах с ограниченымы ресурсами(IoT).

• Если в промежутке [-2,2] кривая сигмоиды изменяет значения “быстро” то по краях фукция остается практически неизменной, это говорит о том, что при высоких порогах, будет крайне сложно получить значения, которые близки к еденице, нейронная сеть будет обучаться долго и малоэфективно. Эта проблема также известна, как проблема изчезающего градиента, так как ближе к границам сигмоидальной функции, градиент стремится к нулю, что в свою очередь рано или поздно приведет к проблемам с плавающей точкой.

Гиперболический тангенс

Гиперболический тангенс - еще одна распространенная функция активации.

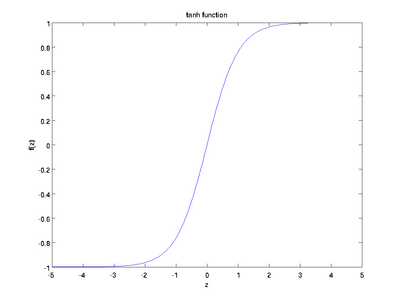
Формула тангенса: $tanh(x) = 2sigmoid(2x) - 1$
Где

$$sigmoid(z^{(i)}) = \frac{1}{1-e^{-z^{(i)}}}$$

По своей сути гиперболический тангенс является модифицированной сигмоидой. Для сравнения покажем на одном графике:

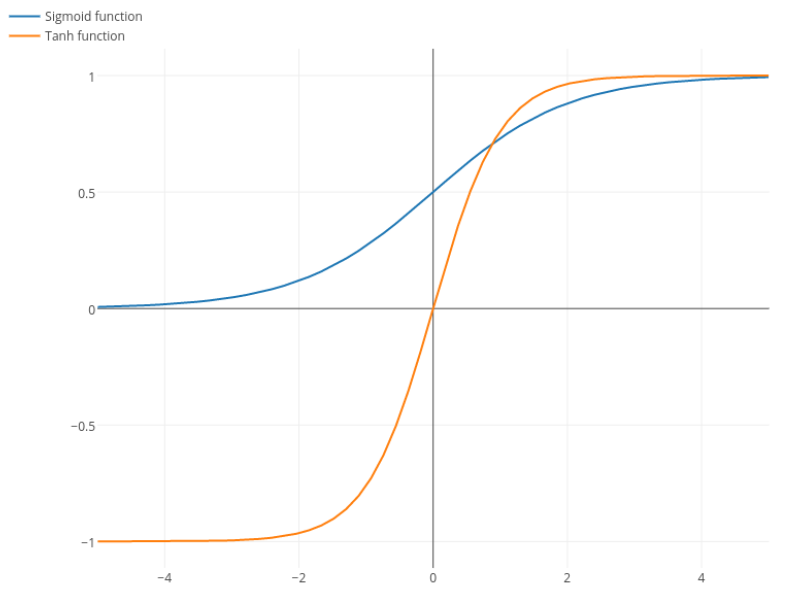
Как можно увидеть на графике, кривая тангенса круче, соответсвенно, более чувствительна к изменениям $x$. Также стоит заметить, что значения функции находятся в границах [-1,1], то есть, $tanh$ имеет большую амплитуду,что является преимуществом, так как значения $y$ для каждого класса лежит в более широком диапазоне.

Функция тангенса подвержена тем же порокам, что и сигмоида, так как имеет с ней общую сущность. На практике активно применяют и сигмоиду и гиперболический тангенс, а что выбрать зависит от конкретной ситуации.

ReLU

ReLU(rectified linear unit) - наиболее часто применяемaя функция активации, в частности в области “компьютерного зрения”.

$$f(x) = max(0,x)$$

ReLu возвращает значение х, если х положительно, и 0 в противном случае.

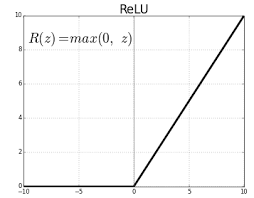
Основное преимущество этой функции - разреженность активации. В случае сигмоиды или $tanh$ все нейроны частично активированы, в то время как ReLU позволяет не активировать некоторые вообще, что ведет к снижению вичислительных затрат, а это как нельзя актуально при обучении глубоких нейронных сетей.

Правда есть и недостатки:

Из-за того, что часть ReLu представляет из себя горизонтальную линию (для отрицательных значений X), градиент на этой части равен 0. Из-за равенства нулю градиента, веса не будут корректироваться во время спуска. Это означает, что пребывающие в таком состоянии нейроны не будут реагировать на изменения в ошибке/входных данных (просто потому, что градиент равен нулю, ничего не будет меняться). Такое явление называется проблемой умирающего ReLu (Dying ReLu problem). Из-за этой проблемы некоторые нейроны просто выключатся и не будут отвечать, делая значительную часть нейросети пассивной. Однако существуют вариации ReLu, которые помогают эту проблему избежать. Например, имеет смысл заменить горизонтальную часть функции на линейную. Если выражение для линейной функции задается выражением y = 0.01x для области x < 0, линия слегка отклоняется от горизонтального положения. Существует и другие способы избежать нулевого градиента. Основная идея >здесь — сделать градиент неравным нулю и постепенно восстанавливать его во время тренировки.

Вот как это выглядит:

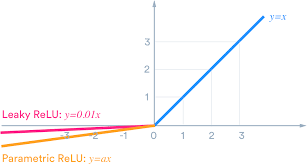
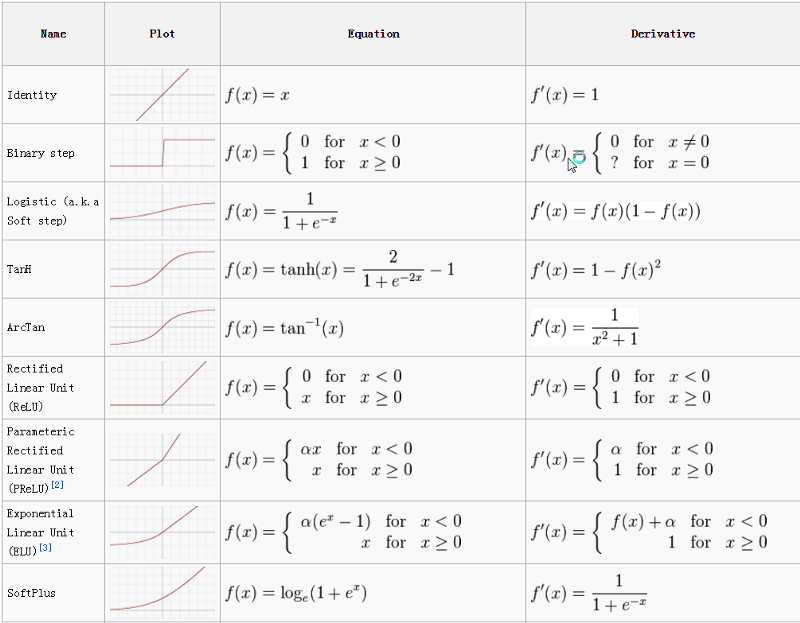
Графики различных ф-ций активации:

Прямое распространение (Forward Propagation)

Прямое распостранение - это собстевенно, пропуск данных через мясорубку скрытых слоев нейронов. Например если у нас три скрытых слоя то, прямое распространие можно описать так:

$$f(x) = f_3(f_2(f_1(x)))$$

Где:

$f_1(x)$: функция выученая на первом слое
$f_2(x)$: функция выученая на втором слое
$f_3(x)$: функция выученая на третьем слое

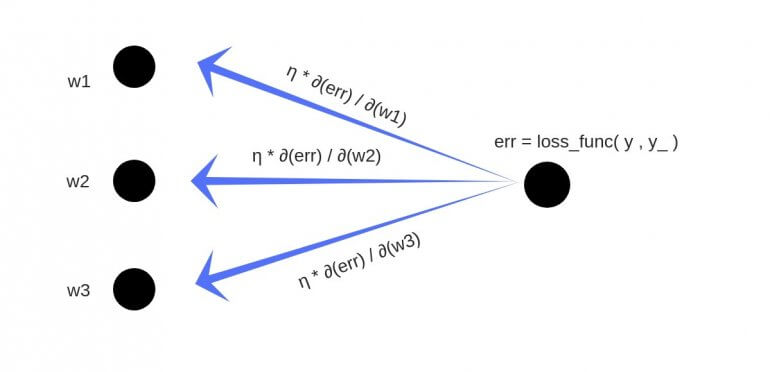
Обратное распостранение

Обратное распостранение представляет собой подсчет ошибки на каждом из слоев и коректирование весов с целью минимизации этой ошибки.

Для этого мы подсчитываем градиент на каждом слое и умножаем эго на скорость обучения(learning rate), штрафуем этим значением вектор параметров для каждого слоя, в итоге добиваясь минимизации ошибки.

Имплементация на Python

def initialize_parameters(layers_dims):
    np.random.seed(1)               
    parameters = {}
    L = len(layers_dims)            

    for l in range(1, L):           
        parameters["W" + str(l)] = np.random.randn(
            layers_dims[l], layers_dims[l - 1]) * 0.01
        parameters["b" + str(l)] = np.zeros((layers_dims[l], 1))

        assert parameters["W" + str(l)].shape == (
            layers_dims[l], layers_dims[l - 1])
        assert parameters["b" + str(l)].shape == (layers_dims[l], 1)
    
    return parameters

Activation function

def sigmoid(Z):
    A = 1 / (1 + np.exp(-Z))
    return A, Z


def tanh(Z):
    A = np.tanh(Z)
    return A, Z


def relu(Z):
    A = np.maximum(0, Z)
    return A, Z


def leaky_relu(Z):
    A = np.maximum(0.1 * Z, Z)
    return A, Z

Visualization:

z = np.linspace(-10, 10, 100)

# Computes post-activation outputs
A_sigmoid, z = sigmoid(z)
A_tanh, z = tanh(z)
A_relu, z = relu(z)
A_leaky_relu, z = leaky_relu(z)

# Plot sigmoid
plt.figure(figsize=(12, 8))
plt.subplot(2, 2, 1)
plt.plot(z, A_sigmoid, label="Function")
plt.plot(z, A_sigmoid * (1 - A_sigmoid), label = "Derivative") plt.legend(loc="upper left")
plt.xlabel("z")
plt.ylabel(r"$\frac{1}{1 + e^{-z}}$")
plt.title("Sigmoid Function", fontsize=16)
# Plot tanh
plt.subplot(2, 2, 2)
plt.plot(z, A_tanh, 'b', label = "Function")
plt.plot(z, 1 - np.square(A_tanh), 'r',label="Derivative") plt.legend(loc="upper left")
plt.xlabel("z")
plt.ylabel(r"$\frac{e^z - e^{-z}}{e^z + e^{-z}}$") plt.title("Hyperbolic Tangent Function", fontsize=16)
# plot relu
plt.subplot(2, 2, 3)
plt.plot(z, A_relu, 'g')
plt.xlabel("z")
plt.ylabel(r"$max\{0, z\}$")
plt.title("ReLU Function", fontsize=16)
# plot leaky relu
plt.subplot(2, 2, 4)
plt.plot(z, A_leaky_relu, 'y')
plt.xlabel("z")
plt.ylabel(r"$max\{0.1z, z\}$")
plt.title("Leaky ReLU Function", fontsize=16)
plt.tight_layout();

Forward Prop

# Define helper functions that will be used in L-model forward prop
def linear_forward(A_prev, W, b):
    Z = np.dot(W, A_prev) + b
    cache = (A_prev, W, b)
    return Z, cache


def linear_activation_forward(A_prev, W, b, activation_fn):
    assert activation_fn == "sigmoid" or activation_fn == "tanh" or \
        activation_fn == "relu"

    if activation_fn == "sigmoid":
        Z, linear_cache = linear_forward(A_prev, W, b)
        A, activation_cache = sigmoid(Z)

    elif activation_fn == "tanh":
        Z, linear_cache = linear_forward(A_prev, W, b)
        A, activation_cache = tanh(Z)

    elif activation_fn == "relu":
        Z, linear_cache = linear_forward(A_prev, W, b)
        A, activation_cache = relu(Z)

    assert A.shape == (W.shape[0], A_prev.shape[1])

    cache = (linear_cache, activation_cache)
    return A, cache


def L_model_forward(X, parameters, hidden_layers_activation_fn="relu"):
    A = X                           
    caches = []                     
    L = len(parameters) // 2        

    for l in range(1, L):
        A_prev = A
        A, cache = linear_activation_forward(
            A_prev, parameters["W" + str(l)], parameters["b" + str(l)],
            activation_fn=hidden_layers_activation_fn)
        caches.append(cache)

    AL, cache = linear_activation_forward(
        A, parameters["W" + str(L)], parameters["b" + str(L)],
        activation_fn="sigmoid")
    caches.append(cache)

    assert AL.shape == (1, X.shape[1])
    return AL, caches

Cost

# Compute cross-entropy cost
def compute_cost(AL, y):
    m = y.shape[1]              
    cost = - (1 / m) * np.sum(
        np.multiply(y, np.log(AL)) + np.multiply(1 - y, np.log(1 - AL)))
    return cost

BackProp

def sigmoid_gradient(dA, Z):
    A, Z = sigmoid(Z)
    dZ = dA * A * (1 - A)

    return dZ


def tanh_gradient(dA, Z):
    A, Z = tanh(Z)
    dZ = dA * (1 - np.square(A))

    return dZ


def relu_gradient(dA, Z):
    A, Z = relu(Z)
    dZ = np.multiply(dA, np.int64(A > 0))

    return dZ


# define helper functions that will be used in L-model back-prop
def linear_backword(dZ, cache):
    A_prev, W, b = cache
    m = A_prev.shape[1]

    dW = (1 / m) * np.dot(dZ, A_prev.T)
    db = (1 / m) * np.sum(dZ, axis=1, keepdims=True)
    dA_prev = np.dot(W.T, dZ)

    assert dA_prev.shape == A_prev.shape
    assert dW.shape == W.shape
    assert db.shape == b.shape

    return dA_prev, dW, db


def linear_activation_backward(dA, cache, activation_fn):
    linear_cache, activation_cache = cache

    if activation_fn == "sigmoid":
        dZ = sigmoid_gradient(dA, activation_cache)
        dA_prev, dW, db = linear_backword(dZ, linear_cache)

    elif activation_fn == "tanh":
        dZ = tanh_gradient(dA, activation_cache)
        dA_prev, dW, db = linear_backword(dZ, linear_cache)

    elif activation_fn == "relu":
        dZ = relu_gradient(dA, activation_cache)
        dA_prev, dW, db = linear_backword(dZ, linear_cache)

    return dA_prev, dW, db


def L_model_backward(AL, y, caches, hidden_layers_activation_fn="relu"):
    y = y.reshape(AL.shape)
    L = len(caches)
    grads = {}

    dAL = np.divide(AL - y, np.multiply(AL, 1 - AL))

    grads["dA" + str(L - 1)], grads["dW" + str(L)], grads[
        "db" + str(L)] = linear_activation_backward(
            dAL, caches[L - 1], "sigmoid")

    for l in range(L - 1, 0, -1):
        current_cache = caches[l - 1]
        grads["dA" + str(l - 1)], grads["dW" + str(l)], grads[
            "db" + str(l)] = linear_activation_backward(
                grads["dA" + str(l)], current_cache,
                hidden_layers_activation_fn)

    return grads

Update parameters

def update_parameters(parameters, grads, learning_rate):
    L = len(parameters) // 2

    for l in range(1, L + 1):
        parameters["W" + str(l)] = parameters[
            "W" + str(l)] - learning_rate * grads["dW" + str(l)]
        parameters["b" + str(l)] = parameters[
            "b" + str(l)] - learning_rate * grads["db" + str(l)]
    return parameters

NN

# Import training dataset
train_dataset = h5py.File("../data/train_catvnoncat.h5")
X_train = np.array(train_dataset["train_set_x"])
y_train = np.array(train_dataset["train_set_y"])

test_dataset = h5py.File("../data/test_catvnoncat.h5")
X_test = np.array(test_dataset["test_set_x"])
y_test = np.array(test_dataset["test_set_y"])

# print the shape of input data and label vector
print(f"""Original dimensions:\n{20 * '-'}\nTraining: {X_train.shape}, {y_train.shape}
Test: {X_test.shape}, {y_test.shape}""")

# plot cat image
plt.figure(figsize=(6, 6))
plt.imshow(X_train[50])
plt.axis("off");

# Transform input data and label vector
X_train = X_train.reshape(209, -1).T
y_train = y_train.reshape(-1, 209)

X_test = X_test.reshape(50, -1).T
y_test = y_test.reshape(-1, 50)

# standardize the data
X_train = X_train / 255
X_test = X_test / 255

print(f"""\nNew dimensions:\n{15 * '-'}\nTraining: {X_train.shape}, {y_train.shape}
Test: {X_test.shape}, {y_test.shape}""")

Ссылки: https://ujjwalkarn.me/2016/08/09/quick-intro-neural-networks/
https://neurohive.io/ru/osnovy-data-science/activation-functions/
https://neurohive.io/ru/osnovy-data-science/osnovy-nejronnyh-setej-algoritmy-obuchenie-funkcii-aktivacii-i-poteri/
https://towardsdatascience.com/activation-functions-neural-networks-1cbd9f8d91d6
https://towardsdatascience.com/coding-neural-network-forward-propagation-and-backpropagtion-ccf8cf369f76