Basic Machine Learning Algos With Python Implementation

Базовые алгоритмы “машинного обучения” и их имплементация с помощью Python

Всем привет, меня зовут Хворостяный Вячеслав. Я работаю аналитиком в компании “Ring Ukraine”, в свободное время занимаюсь изучением алгоритмов “машинного обучения”, являюсь Python энтузиастом. В этой статье я хотел бы поделится с вами примером имплементации базовых алгоритмов МЛ с помощью Python, а также провести их краткий обзор.

Разработки в сфере “машинного обучения” шагнули вперед с ошеломляющей, космической скоростью.Уже сейчас можно применять сложнейшие алгоритмы не особо вникая в суть того, что происходит “под капотом”. Но даже самые сложные системы состоят из атомарных, простейших частиц, которые взаимодействуют между собой.

Каждый из нас уже что-то слышал об “искусственном интеллекте”. ИИ повсюду, это не новость. Прямо сейчас пока я набираю этот текст, алгоритм подсказывает мне где я делаю ошибки, помогает мне подобрать слова, то же самое происходит когда вы набираете текст у себя на смартфоне. Алгоритмы работают на нас когда мы ищем что-то в интернете, читаем почту, смотрим видео на Youtube, ставим лайки в соцсетях. Идеи эти не новы, например старушка Линейная Регрессия, которая будет рассмотрена ниже, впервые была использована Фрэнсисом Гальтоном более 130 лет назад.

В этой статье я покопаюсь в упомянутых “атомах”, попытаюсь немного развеять магическую дымку, овевающую слова “машинное обучение” и “искусственный интеллект”.

Одномерная линейная регрессия

Данный алгоритм является одним из самых широко используемых алгоритмов МЛ, а также самым прозрачным и интерпретируемым. Скорей всего вы уже стыкались с ним в повседневной жизни, а может и применяли на практике. Линейная регрессия это алгоритм позволяющий отобразить линейную зависимость между двумя переменными, выражается формулой: $h = \beta_0 + \beta_1x \\ \tag{1}$ где $h$ - предположение(hypothesis), $(\beta_0, \beta_1)^T$ - вектор параметров, в котором и заключается вся магия, $x$ - независимая переменная

Формула линейной регрессии — это уравнение прямой, коэффициент $\beta_0$ задает смещение этой прямой по оси $y$ , а $\beta_1$ - угол наклона. Вся суть в том, чтобы как можно лучше подобрать параметры $\beta_0$ и $\beta_1$ при заданном $x$ , при этом $h$ будет отображать ожидаемое значение функции.

Линейная регрессия относится к так называемому “обучению с учителем” или “supervised machine learning”, это значит, что у нас уже есть некоторое количество данных где известны как значение аргументов, так и значения самой функции $y$ , наша задача состоит в том чтобы “обучится” на этих, уже размеченных данных, а потом применяя полученный вектор параметров к любому случайному $x$ , получать соответствующий $y$ .

Имея $x$ и $y$ можем рассчитать интересующие нас параметры по формулам:

$\beta_1 = \frac{\sum_{i=1}^{m} (x_i - \bar{x})(y_i - \bar{y})}{\sum_{i=1}^{m} (x_i - \bar{x})^2} \tag{2}$ $\beta_0 = \bar{y} - \beta_1\bar{x}$

Где $\bar{x}$ , $\bar{y}$ - математическое ожидание, оно же среднее арифметическое от векторов $X$ и $Y$
$x_i$ , $y_i$ - элеметы векторов

Данные формулы являются частным случаем метода наименьших квадратов, к которому мы еще вернемся, более подробно о том как выводятся эти формулы можно узнать перейдя по ссылке https://www.wikiwand.com/en/Ordinary_least_squares, ну а если коротко, чтобы получить $\beta_1$ нужно подсчитать все отклонения от среднего для векторов $X$ и $Y$ , в числителе взять суму произведений этих отклонений, а в знаменателе суму квадратов отклонений от среднего по $X$ , $\beta_0$ получаем простой подстановкой.

Имплементация на Python:

import numpy as np
from matplotlib import pyplot as plt 
%matplotlib inline

def ord_LinReg_fit(X,Y):
    x_mean = np.mean(X)
    y_mean = np.mean(Y)

    num = np.sum((X - x_mean)*(Y - y_mean))
    denom = np.sum((X - x_mean)**2)
    
    b_1 = num/denom
    b_0 = y_mean - b_1*x_mean
    return b_0,b_1

# Допустим мы хотим изучить зависимость веса мозгов Y от объёма черепной коробки X
X = np.array([3443, 3993, 3640, 4208, 3832, 3876, 3497, 3466, 3095, 4424]) # см^3
Y = np.array([1340, 1380, 1355, 1522, 1208, 1405, 1358, 1292, 1340, 1400]) # граммы

b0,b1 = ord_LinReg_fit(X,Y) # вычислeние параметров
H = b0 + b1 * X

# Визуализация
plt.plot(X,H, c='b', label='Regression Line')
plt.scatter(X, Y, c='g', label='Known values')

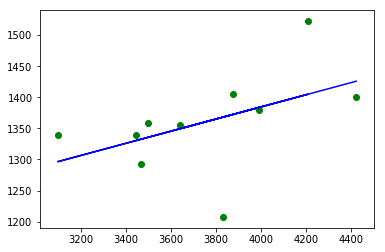
Regression Line

Многомерная линейная регрессия

Многомерную линейную регрессию можно рассматривать как обобщение одномерной, данной выше.

$H = \beta_0x_0 + \beta_1x_1 + \beta_2x_2 + … + \beta_nx_n$ $x_0 = 1$

Единственное изменение состоит в том, что для удобства расчета к первому параметру $\beta_0$ была добавлена еще одна независимая переменная $x_0$ , равна единице.

Уравнение приведенное выше можно записать в свернутой форме как: $H = \theta^TX$

Где

$\theta = [ \theta_0, \theta_1, \theta_2, …, \theta_n ]$ $X = [ x_0, x_1, x_2, …, x_n]$

Согласно методу наименьших квадратов, вектор параметров можно получить путем решения нормального уравнения
$\theta = (X^{T}*X)^{-1}X^{T}Y$

где $\theta$ - вектор параметров

Имплементация на Python:

import numpy as np
from matplotlib import pyplot as 
%matplotlib inline

def get_X_with_ones(X):
    """добавляем столбик единиц"""
    m = len(X)
    X = np.c_[np.ones(m),X]
    return X

def LSM_fit(X,Y):
    X_inv = np.linalg.inv(np.matmul(X.T,X))
    middle_res = np.matmul(X_inv,X.T)
    theta = np.matmul(middle_res,Y)
    return theta

X = np.array([3443, 3993, 3640, 4208, 3832, 3876, 3497, 3466, 3095, 4424]) # см^3
Y = np.array([1340, 1380, 1355, 1522, 1208, 1405, 1358, 1292, 1340, 1400]) # граммы

X_ = get_X_with_ones(X)
theta = LSM_fit(X_,Y)
H = X_.dot(theta.T)

У этого подхода есть несколько недостатков:

Не во всех случаях матрица $(X^{T}*X)^{-1}$ существует
При большом количестве независимых переменных этот способ требует большой вычислительной мощности

Поэтому на практике гораздо чаще можно встретить другой алгоритм вычисления вектора параметров, а именно градиентный спуск.

Градиентный спуск и кост-функция

Градиентный спуск(gradient descent) - алгоритм оптимизации, который позволяет обновлять значения всех элементов вектора параметров одновременно.
Градиент - это вектор частных производных от $\theta$ .
Метод предполагает обновление вектора $\theta$ по всем параметрам, за $n$ шагов.

$J(\theta) = \frac{1}{2m} \sum_{i=1}^{m} (h_\theta(x^{\textrm{(i)}}) - y^{\textrm{(i)}})^2$ $\theta_j := \theta_j - \alpha\frac{\partial}{\partial \theta_j} J(\theta)$ $\theta_j := \theta_j - \alpha\frac{1}{m}\sum_{i=1}^m (h_\theta(x^{(i)})-y^{(i)})x_{j}^{(i)}$

Где
$J(\theta)$ - кост-функция(cost function),
$\alpha$ - так называемый “шаг обучения”(learning rate), его нужно подобрать вручную, так, чтобы $J(\theta)$ достигала минимума при как можно меньшем количестве итераций.
$h_\theta(x^{(i)})$ - гипотеза
$y$ - истинное значение

Так как из $J(\theta) = 0$ вытекает, что гипотеза $h_\theta(x^{(i)})$ полностью совпадает с действительным значением $y$ , задачу метода можно сформулировать как нахождение минимального значения $J(\theta)$ при наименьшем числе итераций. Другими словами, мы подбираем новые коэффициенты с каждой итерацией, пока результат не будет достаточно близок к истинному значению, при этом $J(\theta)$ является индикатором этого приближения.

Метод градиентного спуска широко используется в алгоритмах “машинного обучения”, для решения самых разнообразных задач.

Имплементация на Python:

import numpy as np
from matplotlib import pyplot as plt
%matplotlib inline

def get_X_with_ones(X):
    """нормализируем данные и добавляем столбик единиц"""
    X = np.array(X)
    mean,std = X.mean(), X.std()
    X = (X - mean) / std
    m = len(X)
    X = np.c_[np.ones(m),X].T
    return X

def propagate(theta, X, Y):
    m = X.shape[1]
    H = np.dot(theta.T,X)
    cost = np.sum((H-Y)**2)/(2*m) 
    grads = np.dot(X,(H-Y).T)/m
    return grads, cost

def gradient_descent(X, Y, theta, alpha, iterations):
    cost_hist = []
    for i in range(iterations):
            gradient, cost = propagate(theta, X, Y)
            theta -= alpha*gradient
            cost_hist.append(cost)
    return theta, cost_hist

X = np.array([3443, 3993, 3640, 4208, 3832, 3876, 3497, 3466, 3095, 4424]) # см^3
Y = np.array([1340, 1380, 1355, 1522, 1208, 1405, 1358, 1292, 1340, 1400]) # граммы

alpha = 1
theta = np.zeros((X_.shape[0],1))
X_ = get_X_with_ones(X)
theta, cost_hist = gradient_descent(X_, Y, theta, alpha, 10)
H = np.squeeze(np.dot(theta.T,X_))

Оценка точности модели

Для того чтобы понимать, насколько хорошо или плохо модель справляется с задачей нужно каким то образом оценить результат. В этом нам помогут такие метрики как корень от среднеквадратической ошибки (root mean squared error) и коэффициент детерминации (coefficient of determination).

$RMSE = \sqrt{\sum_{i=1}^{m} \frac{1}{m} (\hat{y_i} - y_i)^2}$ $SS_t = \sum_{i=1}^{m} (y_i - \bar{y})^2$ $SS_r = \sum_{i=1}^{m} (y_i - \hat{y_i})^2$ $R^2 \equiv 1 - \frac{SS_r}{SS_t}$

Где
$RMSE$ - корень от среднеквадратической ошибки(root mean squared error)
$\hat{y_i}$ - гипотеза
$y_i$ - действительное значение
$\bar{y}$ - среднее арифметическое от действительного значения
$R^2$ - коэффициент детерминации

Чем ниже $RMSE$ и чем выше $R^2$ тем лучше модель справляется с задачей. Имплементация на Python:

def rmse(Y, H):
    m = len(Y)
    mse = sum((Y- H)**2)
    rmse = np.sqrt(mse/m)
    return rmse

def r_2(Y,H):
    y_mean = np.mean(Y)
    ss_t = sum((Y - y_mean)**2)
    ss_r = sum((Y - H)**2)
    r_2 = 1 - (ss_r/ss_t)
    return r_2

Применение алгоритмов

Теперь можно попробовать применить рассмотренные алгоритмы на практике и сравнить их с уже готовой имплементацией sklearn. Сделаем это в несколько шагов:

Загружаем датасет и разделяем данные на тренинг-сет и тест-сет, для sklearn нужно правильно задать размерности, метод reshape() помогает справиться с этой задачей.

import pandas as pd
df = pd.read_csv('files/brainhead.csv')

def split_data(df,reshape=False):
    from sklearn.model_selection import train_test_split  
    x = df.values[:, 2] # предпоследняя колонка - объем черепной коробки
    y = df.values[:, 3] # вес мозга
    train_set_x, test_set_x, train_set_y, test_set_y = train_test_split(x, y, test_size=0.33, random_state=42)
    if reshape:
        return (x.reshape(-1,1) for x in [train_set_x, test_set_x, train_set_y, test_set_y])
    return train_set_x, test_set_x, train_set_y, test_set_y

Применяем кастомную модель

import numpy as np

def get_X_with_ones(X):
    """нормализируем данные и добавляем столбик единиц"""
    X = np.array(X)
    mean,std = X.mean(), X.std()
    X = (X - mean) / std
    m = len(X)
    X = np.c_[np.ones(m),X].T
    return X

def propagate(theta, X, Y):
    m = X.shape[1]
    H = np.dot(theta.T,X)
    cost = np.sum((H-Y)**2)/(2*m) 
    grads = np.dot(X,(H-Y).T)/m
    return grads, cost

def gradient_descent(X, Y, theta, alpha, iterations):
    cost_hist = []
    for i in range(iterations):
            gradient, cost = propagate(theta, X, Y)
            theta -= alpha*gradient
            cost_hist.append(cost)
    return theta, cost_hist

def rmse(Y, H):
    m = len(Y)
    mse = sum((Y- H)**2)
    rmse = np.sqrt(mse/m)
    return rmse

def r_2(Y,H):
    y_mean = np.mean(Y)
    ss_t = sum((Y - y_mean)**2)
    ss_r = sum((Y - H)**2)
    r_2 = 1 - (ss_r/ss_t)
    return r_2

train_set_x, test_set_x, train_set_y, test_set_y = load_data(df)
X,Y = train_set_x, train_set_y
X_test = get_X_with_ones(test_set_x)

alpha = 1
X_ = get_X_with_ones(X)
theta = np.zeros((X_.shape[0],1))
theta, cost_hist = gradient_descent(X_, Y, theta, alpha, 20)
H = np.squeeze(np.dot(theta.T,X_test))

print(f'r^2: {r_2(test_set_y,H)} rmse: {rmse(test_set_y,H)}')

Результат: r^2: 0.672757755764332 rmse: 68.54674574377383

Применяем готовую модель с библиотеки

from sklearn.metrics import mean_squared_error
from sklearn.linear_model import LinearRegression

train_set_x, test_set_x, train_set_y, test_set_y = load_data(df, reshape=True)

model = LinearRegression()
model.fit(train_set_x, train_set_y)

y_pred = model.predict(test_set_x)
mse = mean_squared_error(y_pred, test_set_y) 

r_2_sklearn = model.score(train_set_x, train_set_y)
rmse_sklearn = np.sqrt(mse)

print(f'r^2_sklearn: {r_2_sklearn}, rmse_sklearn: {rmse_sklearn}')

Результат: r^2_sklearn: 0.6236128413780265, rmse_sklearn: 68.91317515113433

В итоге у кастомной модели немного меньше ошибка и соответственно выше коэффициент детерминации.

В этой статье были приведены базовые алгоритмы “машинного обучения” и их имплементация на Python, а уже в следующей, будет рассмотрен алгоритм логистической регрессии для решения задач классификации объектов.

Для написания этой статьи использовались материалы:
https://mubaris.com/posts/linear-regression/
https://www.wikiwand.com/en/Ordinary_least_squares
https://www.coursera.org/learn/machine-learning

Ссылка на датасеты и многое другое: https://www.kaggle.com/datasets
Ссылка на проект: https://github.com/vkhvorostianyi/ML_blog/tree/master/articles/linear_regression